UWB是目前比较热门也是比较成熟的高精准定位方式。最常用的算法就是chan算法。网络上很多相关文章和资料，但是也比较混乱，大部分是研究生研究学习编写的，所以基于实际的使用，在此列出学习理解的步骤：

此为matlab源代码：(以下代码均已经过C++编码的验证)

Chan3D.m

function [X] = Chan3D(BSN,BS,R)
 
%% 第一次WLS
 
 %k=X^2+Y^2+Z^2
for i = 1:BSN                      %BSN为基站个数
    k(1,i) = BS(1,i)^2 + BS(2,i)^2 + BS(3,i)^2;  %BS为基站坐标
end
 
%h = 1/2(Ri^2-ki+k1)
for i =1:BSN-1
    h(i,1) = 0.5*(R(i)^2 - k(1,i+1) + k(1,1));  %注意k(i+1)
end
 
 
%Ga = [Xi,Yi,Zi,Ri]
for i = 1:BSN-1
    Ga(i,1) = -BS(1,i+1);
    Ga(i,2) = -BS(2,i+1);
    Ga(i,3) = -BS(3,i+1);
    Ga(i,4) = -R(i);
end
 
%Q为TDOA系统的协方差矩阵
Q = cov(R);
 
%MS与BS距离较近时
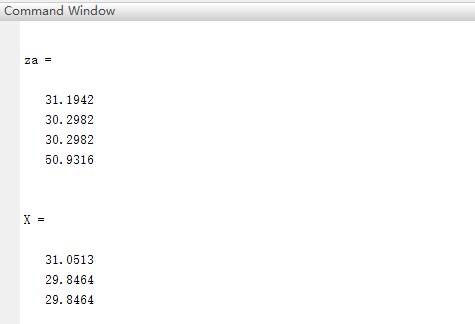
za = pinv(Ga' * inv(Q) * Ga) * Ga' * inv(Q) * h
 
%% 第二次WLS
%h'
X1 = BS(1,1);
Y1 = BS(2,1);
Z1 = BS(3,1);
h2 = [
    (za(1,1) - X1)^2;
    (za(2,1) - Y1)^2;
    (za(3,1) - Z1)^2;
     za(4,1)^2
      ];
 
%Ga'
Ga2 = [
    1,0,0;
    0,1,0;
    0,0,1;
    1,1,1
    ];
 
%B'
B2 = [
      za(1,1)-X1,0,0,0;
      0,za(2,1)-Y1,0,0;
      0,0,za(3,1)-Z1,0;
      0,0,0,za(4,1)
      ];
  
%za',距离较远时
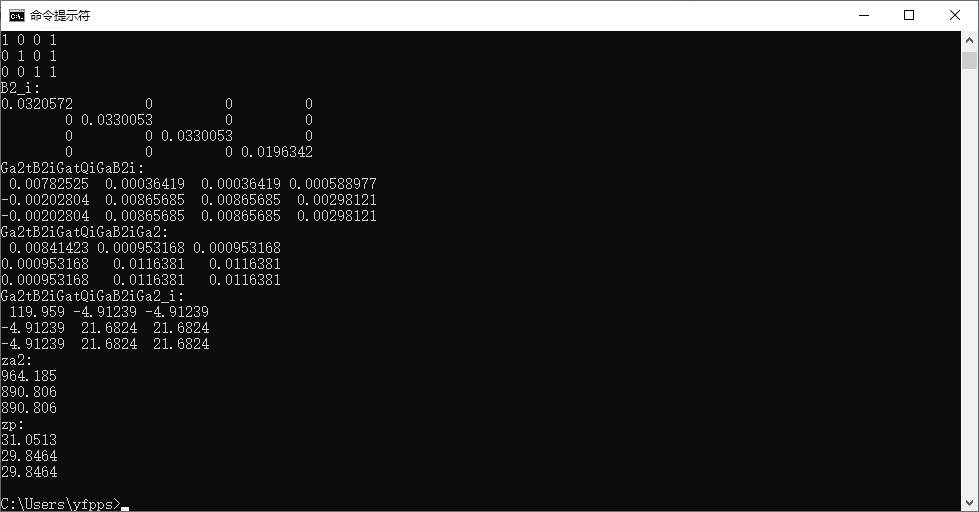
za2 = pinv( Ga2' * inv(B2) * Ga' * inv(Q) * Ga * inv(B2) * Ga2) * (Ga2' * inv(B2) * Ga' * inv(Q) * Ga * inv(B2)) * h2;
 
zp(1,1) = abs(za2(1,1))^0.5 + X1;
zp(2,1) = abs(za2(2,1))^0.5 + Y1;
zp(3,1) = abs(za2(3,1))^0.5 + Z1;
 
X = zp;
 
end

Chan3dtest.m

BSN = 6;%基站数目
%各个基站的位置，3*BSN的矩阵存储，每一列是一个坐标
BS = [
        0 , sqrt(3) , 0.5*sqrt(3) , -0.5*sqrt(3) , -sqrt(3) , -0.5*sqrt(3) , 0.5*sqrt(3); 
        0 ,       0 ,         1.5 ,         1.5  ,        0 ,        -1.5  ,        -1.5; 
        0 ,       0 ,         1.5 ,         1.5  ,        0 ,        -1.5  ,        -1.5
      ];
BS = BS(:,1:BSN);
BS = BS .* 50;
 
%MS的实际距离,为待测量值
MS = [30,30,30];
 
% R0为无噪声情况下各个BS与MS的距离
for i = 1:BSN
    R0(i) = sqrt((BS(1,i)-MS(1))^2 + (BS(2,i)-MS(2))^2 + (BS(3,i)-MS(3))^2);
end
 
%噪声方差
Noise = 1;
%R（i）,是加上噪声后，BSi与BS1到MS的距离差，实际中应由TDOA*c算得（基站和移动台送出的数据计算）
%for i = 1:BSN-1
%    R(i) = R0(i+1) - R0(1) + Noise * randn(1);
%end
R = [17.3477082749703,13.0324148452678,44.5503414498834,74.2974876429252,114.776084308268;]
 
X = Chan3D(BSN,BS,R)

Chan3D算法经过两次WLS最小二乘法运算，我们可以看到